01-哥德巴赫猜想 (Goldbach's Conjecture)
目录
前言
哥德巴赫猜想是(Goldbach’s Conjecture)是数论中存在最久的未解问题之一,
是一个伟大的世界性的数学猜想,其基本思想可以陈述为:
任何一个大于2的偶数,都能表示成两个素数之和。
如:
4 = 2 + 2
6 = 3 + 3
96= 23 + 73
本文将采用两种不同的算法来求出给定范围 n 内的哥德巴赫数字,并对比其时间复杂度,得出更优算法。
分析
根据哥德巴赫猜想,我们可以得出如下信息:
- 哥德巴赫数字是一个大于2的偶数。
- 哥德巴赫数字等于两个素数相加。
思路A
思路A与之前见过的很多想法一样,简单粗暴,采用嵌套 for 循环。思路如下:
- for 循环依次遍历 [4, n] 范围内的偶数。
- 然后,针对每个数字(c)再次进行 for 循环找出两个数字(a,b)之和等于该数字的数字。(即 c = a + b)
- 判断 a,b 是否都为素数。
- 输出结果。
Show the (garbage) code!
实现A
我们把思路A实现的程序分成两个功能模块:
判断是否为素数模块 int isPrime(int i),返回 1 即为素数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int isPrime(int i) {
int j;
if (i <= 1) return 0;
if (i == 2) return 1;
for (j = 2; j < i; j ++) {
number ++;
if (i % j == 0) {
return 0;
}else if(i != j + 1) {
continue;
}else {
return 1;
}
}
}
主程序模块:针对 [4, n] 之间的正偶数进行数值拆分,然后再用isPrime函数进行筛选,如果k,j都为素数,即满足哥德巴赫猜想,输出该数字。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16do {
printf("please enter a number:");
int number = 0;
scanf("%d", &number);
int i, j, k;
for (int i = 4; i <= number; i += 2) {
for (k = 2; k<= i/2; k ++) {
j = i - k;
if (isPrime(k)) {
if (isPrime(j)) {
printf("%d=%d+%d\n",i, k, j);
}
}
}
}
}while (1);
思路B
递归算法,也是我业余时间自己写的一个,递归路径类似鱼骨头,基本思路如下:
- 针对输入的 n 进行拆分(c = a + b 的形式)并递归。
- 如果拆分的数字 a,b 为偶数,则可能为符合哥德巴赫猜想,回到1。
- 如果 c 为偶数,且 a,b 为素数,即满足哥德巴赫猜想,输出该数字。
这里笔者画了一张抽象的鱼骨头图,帮助读者理解:
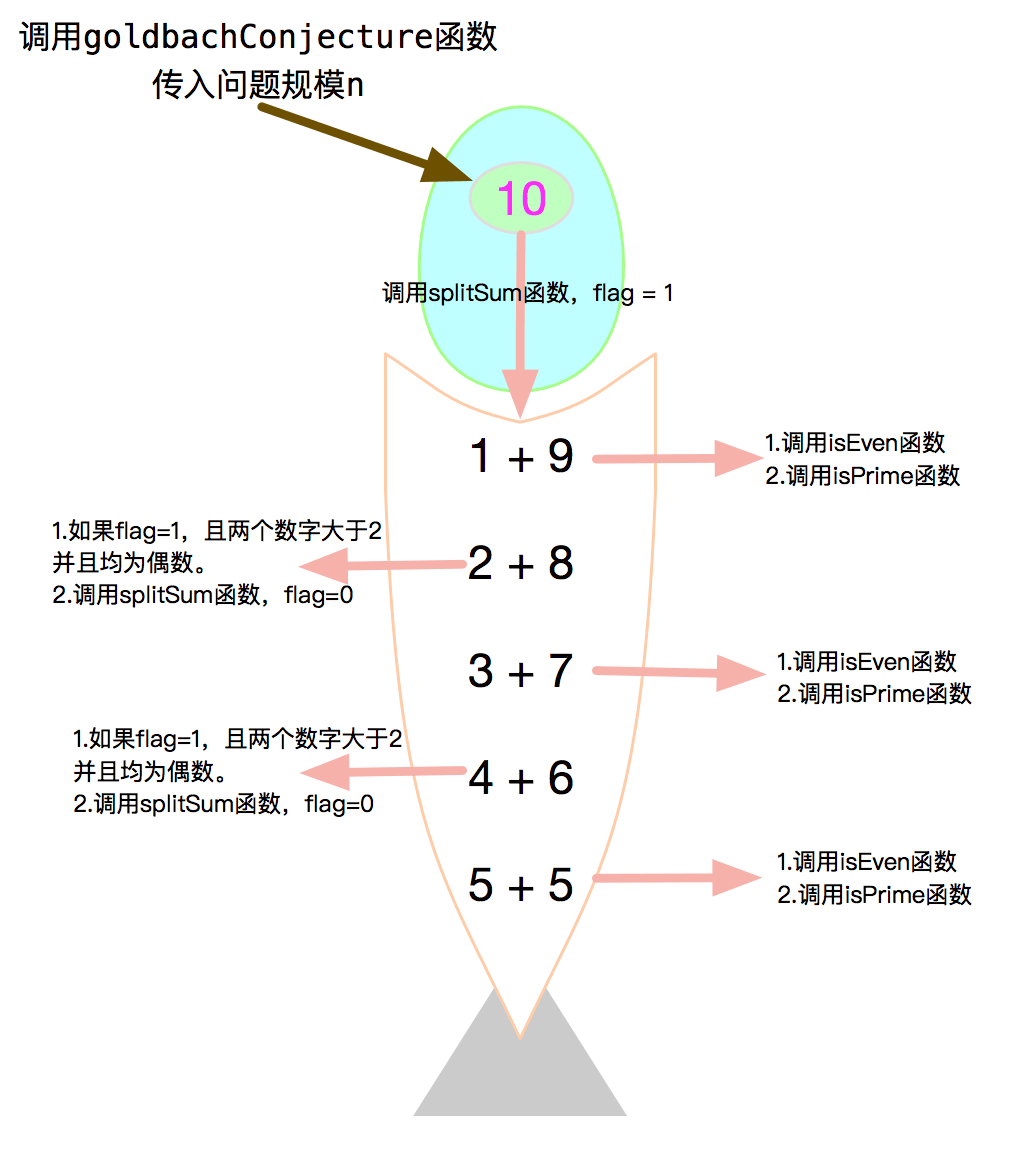
实现B
思路B实现的程序主要分成三个功能模块,为了区分思路A,判断素数的模块也采用递归的形式:
判断是否为素数 int isPrime(int i),返回 1 即为素数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 判断偶数
int isEven(int original) {
return (original % 2 == 0);
}
int isPrimeInner(int original, int current) {
if (current<=0 || original<=0 || original == 1) return 0;
if (original % 2 == 0) {
if (original == 2) return 1;
return 0;
}
if (current > (original / 2) + 1) return 1;
if (original % current == 0 && current != 1) return 0;
return isPrimeInner(original, current + 2);
}
// 判断是否为偶数
int isPrime(int original) {
return isPrimeInner(original, 1);
}递归模块
参数
current: 代表分裂初始值,参数flag: 代表是否深入遍历,此处用于控制重复遍历的情况,如:original=10 时,second=8 时,两次会都会重复遍历 6/4/2,因此加入flag进行限制,只进行一次深入遍历!!1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
void splitSumInner(int c, int current, int flag) {
// 哥德巴赫为大于2的偶数
if (c <= 2) return;
// 如果 current 大于 c 的一半,即代表遍历完毕
if (current >= (c / 2) + 1) return;
// 第一次分裂 c 数值
int a = current;
int b = c - current;
// 递归遍历并分裂 c 数值
splitSumInner(c, ++ current, flag);
// 判断能否深入遍历
if (flag && a > 2 && isEven(a)) {
// 深入遍历 分裂第一个子偶数
splitSum(a, 0);
}
if (flag && b > 2 && isEven(b)) {
// 深入遍历 分裂第二个子偶数
splitSum(b, 0);
}
// 如果 c 为偶数,且 a,b 为素数,即满足哥德巴赫猜想,输出该数字。
if (isEven(c) && isPrime(a) && isPrime(b)) {
printf("\n%d=%d+%d\n",c, a, b);
}
}
// original: 待分裂的原始数值(ps:会自动分裂 小于 original 下的所有数值)
// flag: 1 代表分裂小于 original 下的所有数值;0 代表分裂当前 original 数值
void splitSum(int original, int flag) {
splitSumInner(original, 1, flag);
}主程序模块
1
2
3
4
5
6
7
8
9
10
11
12
13
14
void goldbachConjecture(int n) {
splitSum(n, 1);
}
int main() {
do {
printf("please enter a number:");
int number = 0;
scanf("%d", &number);
goldbachConjecture(number);
} while (1);
return 0;
}
时间复杂度对比
时间复杂度说白了就是算法中基本操作的执行次数,更通俗的说法,就是最深层循环内的语句。基本操作的重复执行次数是和算法的执行时间成正比的。下面我们来粗略计算一下上述算法的时间复杂度。
A 算法分析
在程序 A 中,与下面的代码相同,采用嵌套三层 for 循环的方式进行遍历:
1
2
3
4
5
6
7
8
9
for (int i = 1; i <= n; i ++) { // 第一层循环
for (int j = 1; j <= i; j ++) { // 第二层循环
for (int k = 1; k <= j; k ++) { // 第三层循环
count ++;
printf("%d*%d*%d\n", i, j, k);
}
}
}
下面我们来剖析一下基本操作:
- 第一层 for 循环执行 n 次。
- 第二层 for 循环以 i 为规模分别执行 1,2,3,4……n-1,n 次,集一个公差为 1 的等差数列,总次数为 (n+1)*n/2。
第三层 for 循环采用排列组合来计算,举个例子,当 n = 3 时,有 10 次基本操作,我们把执行路径格式定义成 ijk,如下:
1
2
3
4
111
211 221 222
311 321 322 331 332 333

B 算法分析

结论
以上时间复杂度只是笔者通过简单粗略的分析得出,仅供参考。通过上述分析,我们发现算法A与算法B时间复杂度是一样的,感兴趣的童鞋可以自己计算上述两种算法的时间复杂度。笔者通过测试发现,相同的问题规模,随着 n 的增大,算法B的时间复杂度要远小于算法A。如:n = 100 时,算法B遍历次数是 6380 次左右,算法A遍历次数高达 15569 次(论算法糟糕的可怕性…)。源码地址
广告
欢迎关注微信公众号